
IV. От одноступенчатой к многоступенчатой ракете
На рис. 22 показано, что траектория баллистической ракеты, а следовательно, и дальность ее полета зависит от начальной скорости V0 и угла Θ0 между этой скоростью и горизонтом. Этот угол называется углом бросания.
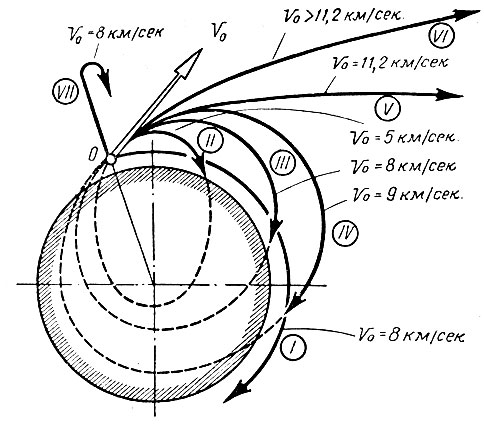
Рис. 22. Траектории полета ракеты при различных углах бросания и начальных скоростях
Пусть, например, угол бросания равен Θ0 = 30°. В этом случае ракета, начавшая свой баллистический полет в точке 0 со скоростью V0 = 5 км/сек, пролетит по эллиптической кривой II. При V0 = 8 км/сек ракета пролетит по эллиптической кривой III, при V0 = 9 км/сек - по кривой IV. Когда скорость будет увеличена до 11,2 км/сек, траектория из замкнутой эллиптической кривой превратится в незамкнутую параболическую и ракета уйдет из сферы притяжения земли (кривая V). При еще большей скорости уход ракеты будет совершаться по гиперболе (VI). Так меняется траектория ракеты при изменении начальной скорости, хотя угол бросания остается неизменным.
Если сохранять постоянной начальную скорость, а менять только угол бросания, то траектория ракеты будет претерпевать не менее значительные изменения.
Пусть, например, начальная 'скорость равна V0 = 8 км/час. Если ракету запустить вертикально вверх (угол бросания Θ0 = 90°), то теоретически она поднимется на высоту, равную радиусу Земли, и вернется на Землю недалеко от старта (VII). При Θ0 = 30° ракета полетит по уже рассмотренной нами эллиптической траектории (кривая III). Наконец при Θ0 = 0° (запуск параллельно горизонту) ракета превратится в спутника Земли с круговой орбитой (кривая I).
Эти примеры показывают, что только путем изменения угла бросания дальность ракет при той же начальной скорости 8 км/сек может иметь диапазон от нуля до бесконечности.
Под каким углом ракета начнет свой баллистический полет? Это зависит от программы управления, которая задана ракете. Можно, например, для каждой начальной скорости выбрать наивыгоднейший (оптимальный) угол бросания, при котором дальность полета будет наибольшей. По мере увеличения начальной скорости этот угол уменьшается. Получающиеся при этом примерные значения дальности, высоты и времени полета показаны в табл. 4.
Таблица 4
| Начальная скорость, км/сек | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Оптимальный угол бросания° | 44,8 | 44,3 | 42,6 | 41,0 | 38,5 | 33,5 | 26,0 | 0,0 |
| Дальность полета, км | 100 | 500 | 1000 | 1 800 | 3 200 | 6 000 | 9 000 | Спутник Земли |
| Максимальная высота траектории, км | 50 | 160 | 300 | 400 | 500 | 880 | 1 300 | Заданная |
| Время полета, мин | 2,6 | 7,0 | 9,2 | 11,5 | 16,0 | 22,0 | 32,0 | Зависит от высоты |
Если угол бросания можно менять произвольно, то изменение начальной скорости ограничено, и увеличение ее на каждый 1 км/сек связано с большими техническими проблемами.
К. Э. Циолковским дана формула, позволяющая определить идеальную* скорость ракеты в конце ее разгона двигателями:
Vид = Vист · ln · Gнач/Gкон,
где Vид - идеальная скорость ракеты в конце активного участка;
Vист - скорость истечения газов из реактивного сопла двигателя;
Gнач - начальный вес ракеты;
Gкон - конечный вес ракеты;
ln - знак натурального логарифма.
С величиной скорости истечения газов из сопла ракетного двигателя мы познакомились в предыдущем разделе. Для жидких топлив, приведенных в табл. 3, эти скорости ограничены величиной 2200 - 2600 м/сек (или 2,2 - 2,6 км/сек), а для твердых топлив - величиной 1,6 - 2,0 км/сек.
Gнач обозначает начальный вес, т. е. полный вес ракеты перед стартом, а Gкон - ее конечный вес в конце разгона (после израсходования топлива или выключения двигателей). Отношение этих весов Gнач/Gкон, входящее в формулу, называется числом Циолковского и косвенно характеризует вес топлива, израсходованного на разгон ракеты. Очевидно, чем больше число Циолковского, тем большую скорость разовьет ракета и, следовательно, тем дальше она пролетит (при прочих равных условиях), Однако число Циолковского, так же как и скорость истечения газов из сопла, имеет свои ограничения.
На рис. 23 показаны разрез типовой одноступенчатой ракеты и ее весовая схема. Помимо баков с топливом, на ракете имеются двигатели, органы и системы управления, обшивка, полезный груз, имеются там и различные конструктивные элементы, вспомогательное оборудование. Поэтому конечный вес ракеты не может быть во много раз меньше ее начального веса. Например, немецкая ракета V-2 весила без топлива 3,9 т, а с топливом 12,9 т. Значит число Циолковского этой ракеты было равно: 12,9/3,9 = 3,31. На современном уровне развития зарубежного ракетостроения это отношение у иностранных ракет достигает величины 5 - 7.
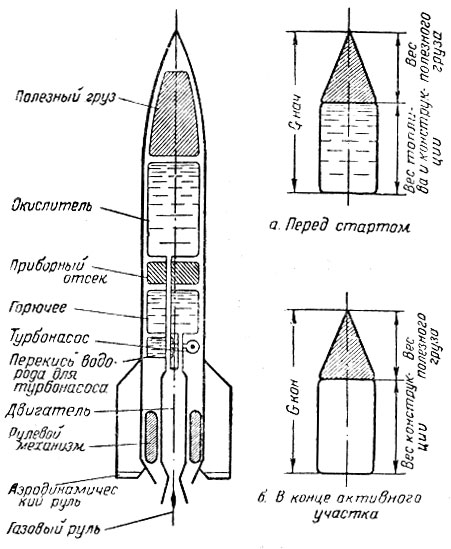
Рис. 23. Разрез типовой одноступенчатой ракеты и ее весовая схема
Подсчитаем идеальную скорость одноступенчатой ракеты, приняв V0 = 2,6 км/сек. и Gнач/Gкон = 7,
Vид = 2,6 · ln 7 = 2,6 · 1,946 ≈ 5 км/сек.
Из табл. 4 видно, что такая ракета способна достичь дальности порядка 3 200 км. Однако ее фактическая скорость будет меньше 5 км/сек. поскольку двигатель расходует свою энергию не только на разгон ракеты, но и на преодоление сопротивления воздуха, на преодоление силы земного притяжения. Фактическая скорость ракеты составит всего 75 - 80% от идеальной. Следовательно, она будет иметь начальную скорость около 4 км/сек и дальность не более 1800 км*.
*(Дальность, приведенная в табл. 4, дана приближенно, поскольку при ее подсчете не учитывался ряд факторов. Например, не учитывались участки траектории, лежащие в плотных слоях атмосферы, влияние вращения Земли. При стрельбе в восточном направлении дальность полета баллистических ракет получается большей, так как к их скорости относительно Земли прибавляется скорость вращения самой Земли.)
Для создания межконтинентальной баллистической ракеты, запуска искусственных спутников Земли и космических кораблей, а тем более для посылки космических ракет на Луну и планеты необходимо сообщить ракете-носителю значительно большую скорость. Так, для ракеты с дальностью 9000 - 13000 км необходима начальная скорость порядка 7 км/сек. Первая космическая скорость, которую необходимо сообщить ракете, чтобы она могла стать спутником Земли с малой высотой орбиты, равна, как известно, 8 км/сек.
Для выхода из сферы притяжения Земли ракету надо разогнать до второй космической скорости - 11,2 км/сек, для облета Луны (без возвращения на Землю) требуется скорость более 12 км/сек. Облет Марса без возвращения на Землю можно осуществить при начальной скорости около 14 км/сек, а с возвращением на орбиту вокруг Земли - около 27 км/сек. Скорость 48 км/сек требуется для сокращения продолжительности полета к Марсу и обратно до трех месяцев. Увеличение скорости ракеты, в свою очередь, требует расходования все возрастающего количества топлива на разгон.
Пусть, например, мы построили ракету, весящую без топлива 1 кг. Если мы захотим сообщить ей скорость 3, 6, 9 и 12 км/сек, то сколько топлива потребуется для этого заправить в ракету и сжечь при разгоне? Необходимое количество топлива* показано в табл. 5.
*(При скорости истечения 3 км/сек.)
Таблица 5
| Чтобы разогнать 1 кг груза до идеальной скорости, равной | Надо израсходовать топлива (округленно), кг |
| 3 км/сек | 1,7 |
| 6 " | 6,4 |
| 9 " | 19 |
| 12 " | 54 |
Не подлежит сомнению, что в корпусе ракеты, "сухой" вес которой равен всего 1 кг, нам удастся вместить 1,7 кг топлива. Но очень сомнительно, что в ней можно разместить его 6,4 кг. И, очевидно, совершенно невозможно заправить в нее 19 или 54 кг топлива. Простой, но достаточно прочный бак, вмещающий такое количество топлива, весит уже значительно больше килограмма. Например, известная автомобилистам двадцатилитровая канистра весит около 3 кг. "Сухой" же вес ракеты, помимо бака, должен включать в себя вес двигателей, конструкции, полезного груза и т. д.
Наш великий соотечественник К. Э. Циолковский нашел другой (и пока единственный) путь, позволяющий решить такую трудную задачу, как достижение ракетой тех скоростей, которые сегодня требуются практикой. Этот путь состоит в создании многоступенчатых ракет.
Типовая многоступенчатая ракета изображена на рис. 24. Она состоит из полезного груза И нескольких отделяемых ступеней с силовой установкой и запасом топлива в каждой. Двигатель первой ступени сообщает полезному грузу, а также второй и третьей ступеням (второй субракете) скорость ν1. После израсходования топлива первая ступень отделяется от остальной части ракеты и падает на землю, а на ракете включается двигатель второй ступени. Под действием его тяги оставшаяся часть ракеты (третья субракета) приобретает дополнительную скорость ν2. Затем вторая ступень после израсходования топлива также отделяется от оставшейся части ракеты и падает на землю. В это время включается двигатель третьей ступени и сообщает полезному грузу добавочную скорость ν3.
Таким образом, в многоступенчатой ракете полезный груз разгоняется многократно. Полная идеальная скорость трехступенчатой ракеты будет равна сумме трех идеальных скоростей, полученных от каждой ступени:
Vид3 = ν1 + ν2 + ν3.
Если скорость истечения газов из двигателей всех ступеней одинакова и после отделения каждой из них не меняется отношение начального веса оставшейся части ракеты к конечному, то приросты скорости ν1, ν2 и ν3 будут равны между собой. Тогда можно считать, что скорость ракеты, состоящей из трех (или вообще п) ступеней, будет равна утроенной (или увеличенной в n раз) скорости одноступенчатой ракеты.
Фактически в каждой ступени многоступенчатых ракет могут стоять двигатели, дающие разные скорости истечения; постоянное отношение весов может не выдерживаться; сопротивление воздуха по мере изменения скорости полета и притяжение Земли по мере удаления от нее изменяются. Поэтому конечная скорость многоступенчатой ракеты не может быть определена простым умножением скорости одноступенчатой ракеты на число ступеней*. Но остается справедливым, что путем увеличения числа ступеней скорость ракеты может быть увеличена во много раз.
*(Следует также иметь в виду, что между выключением одной ступени и включением другой может быть временной интервал, в течение которого ракета летит по инерции.)
Кроме того, многоступенчатая ракета может обеспечить заданную дальность полета одного и того же полезного груза при значительно меньшем общем расходе топлива и стартовом весе, чем одноступенчатая ракета. Неужели человеческий разум сумел обойти законы природы? Нет. Просто человек, познав эти законы, может экономить на топливе и весе конструкции, выполняя поставленную задачу. В одноступенчатой ракете мы от самого старта и до конца активного участка разгоняем весь ее "сухой" вес. В многоступенчатой ракете мы этого не делаем. Так, в трехступенчатой ракете вторая ступень уже не тратит топлива на разгон "сухого" веса первой ступени, ибо последняя отбрасывается. Третья ступень также не тратит топлива на разгон "сухого", веса первой и второй ступеней. Она разгоняет только себя и полезный груз. Третью (и вообще последнюю) ступень можно было бы уже не отсоединять от головной части ракеты, потому что дальнейшего разгона не требуется. Но во многих случаях она все же отделяется. Так, отделение последних ступеней практикуется у ракет-носителей спутников, космических ракет и таких боевых ракет, как "Атлас", "Титан", "Минитмэн", "Юпитер", "Поларис" и др.
Когда в космос запускается научная аппаратура, помещенная в головной части ракеты, то предусматривается отделение последней ступени. Это необходимо для правильного функционирования аппаратуры. Когда запускается спутник, также предусматривается его отделение от последней ступени. Благодаря этому уменьшается сопротивление и он может существовать длительное время. При запуске боевой баллистической ракеты предусматривается отделение последней ступени от боевой головки, вследствие этого труднее становится обнаружить боевую головку и попасть в нее антиракетой. Более того, отделившаяся при снижении ракеты последняя ступень становится ложной целью. Если при возвращении в атмосферу предусмотрено управлять боевой головкой или стабилизировать ее полет, то без последней ступени управлять ею легче, так как она обладает меньшей массой. Наконец, если последнюю ступень не отделить от боевой головки, то надо будет защищать ту и другую от нагрева и сгорания, что невыгодно.
Безусловно, задача получения высоких скоростей движения будет решаться не только созданием многоступенчатых ракет. Этот способ имеет и свои недостатки. Дело в том, что с увеличением числа ступеней сильно осложняется конструкция ракет. Появляется необходимость в сложных механизмах для отделения ступеней, Поэтому ученые всегда будут стремиться к минимальному числу ступеней, а для этого, прежде всего необходимо научиться получать все большие и большие скорости истечения продуктов сгорания или продуктов какой-либо другой реакции.
|
ПОИСК:
|
© WEAPONS-WORLD.RU, 2001-2020
При использовании материалов активная ссылка обязательна:
http://weapons-world.ru/ 'Оружие и военная история'
При использовании материалов активная ссылка обязательна:
http://weapons-world.ru/ 'Оружие и военная история'